Lambda Calculus

Table of contents

• Scoping
  • Static Scoping
  • Dynamic Scoping
• Lambda Calculus
  • Concrete Syntax
  • Currying / Multi-argument functions
  • Free and Bound Variables
  • Beta Reductions
  • Alpha Reductions
  • Evaluating a Lambda Expression
  • Normal Form
  • Relating this to our interpreter
• Reduction Strategy
• Encoding programs in Lambda Calculus
  • Encoding Let Bindings
  • Encoding Conditionals and Boolean Values
• Y-Combinator

In the previous module, we concluded by designing a language that has first-class functions and said this language is a general purpose computing langauge. In this module we will take a look at the various design decisions we have made along the way, and what could have been some alternatives and their repercussions. Finally, we will show how even a reduced subset of our language can express all computations using the Lambda Calculus model and so can our language.

Scoping

Scope rules define the visibility rules for identifiers in a programming language. If you have a variable x being referenced in different parts of a program, which definition of x is being referenced? When does the same identifier refer to the same variable or to different ones?

Static Scoping

Most languages, including C, C++, Scheme, Python, JavaScript, and Haskell, are statically scoped. In our languages sub-expression defines a new scope, but in many imperative languges (like C, JavaScript, etc.) blocks define new scopes. Variables can be declared in that scope, and aren’t visible from the outside. However, variables outside the scope – in enclosing scopes – are visible unless they are overridden. In Javascript, Haskell, and Scheme (but not C or C++) these scope rules also apply to the names of functions and procedures.

Static scoping is also sometimes called lexical scoping.

Let us try to understand this with an example:

(let ((m 50))
  (let ((n 100))
    (let ((hardy (λ () n)))
      (let ((laurel (λ (n) (+ m (hardy)))))
        (let ((n 50))
          (+ (laurel 1) (hardy)))))))

The above program defined m and n to be 50 and 100 respectively. Following that we define two functions laurel and hardy. hardy returns n even though n is not passed as an argument to hardy or declared inside it’s definition. Similarly, laurel takes an argument n but adds m to the result of calling hardy. Where will the values of m and n come from when we run these functions? Following that, we redefine n to be 50 and add the result of calling laurel with 1 with hardy. Take a minute to think what the result will be.

You can actually run this program in Racket and find that it evaluates to 250. Why is that? Let us run this program through our Lambda interpreter as well.

> (interp-err (parse-prog '((let ((m 50))
  (let ((n 100))
    (let ((hardy (λ () n)))
      (let ((laurel (λ (n) (+ m (hardy)))))
        (let ((n 50))
          (+ (laurel 1) (hardy))))))))))

250

The interpreter we developed matches the behavior of Racket. Here is what interp-lam looks like in our interpreter:

(define (interp-lam D E S xs body)
  (λ (aargs)
    (interp D (append (zip xs aargs) E) S body)))

It captures the environment E when a lambda is defined and body of the lambda is evaluated in that environment. Thus, anytime a variable is used it looks up local defintions followed by the definitions that came before it. Thus through the example program, in laurel m = 50 and in hardy n = 100. Static scoping allows one to find the values of the variables based on their definitions.

Dynamic Scoping

An alternative to this design decision is dynamic scoping. Dynamic scoping was used in early dialects of Lisp, and some older interpreted languages such as SNOBOL and APL. It is available as an option in Common Lisp. Using this scoping rule, we first look for a local definition of a variable. If it isn’t found, we look up from the calling location rather the location of the definition.

Let us understand this with the same Laurel and Hardy example. Under dynamic scoping, when the hardy function is called, it does not look up the definition of n based on where hardy is defined but where it is called. So to find the value you have to trace the function calls now:

(+ (laurel 1) (hardy)) ; n = 50
      |         |
      |         +--> n = 50
      |
      +-----> (+ m (hardy)) ; n = 1
              (+ 50 1)

As you can see, based on the where the function calls happen, the lookup results change. Thus the above expression results in the value of 101.

As you can see, dynamic scoping is confusing and that is the prime reason why it is out of fashion. One of the perks of having our own interpreter is we can now change the behavior of the language to have dynamic scope. It requires a minor change in the following two functions:

(define (interp-lam D E S xs body)
  (λ (E aargs)
    (interp D (append (zip xs aargs) E) S body)))

(define (interp-app D E S f es)
    (let ([fn   (interp D E S f)]
          [args (map (λ (arg) (interp D E S arg)) es)])
         (fn E args)))

We are now explicitly passing the environment anytime a function is called. This means whenever a variable is looked up, it will walk through the environment based on the calling-site.

That is all we need. We can run the same program through the modified interpreter:

> (interp-err (parse-prog '((let ((m 50))
  (let ((n 100))
    (let ((hardy (λ () n)))
      (let ((laurel (λ (n) (+ m (hardy)))))
        (let ((n 50))
          (+ (laurel 1) (hardy))))))))))

101

We just changed the semantics of the language by making a change in the scoping rules. We did not need to add any new syntax or parsing for this. Tiny decisions we make about the semantics can affect how our programs behave. For now, we will stick to static scoping.

Lambda Calculus

The lambda calculus was introduced in the 1930s by the logician Alonzo Church at Princeton University as a mathematical system for defining computable functions. Alan Turing (who was Church’s Ph.D. student) showed that the lambda calculus is equivalent in definitional power to Turing machines. The lambda calculus serves as the model of computation for functional programming languages and has applications to artificial intelligence, proof systems, and logic.

The programming language Lisp was developed by John McCarthy at MIT in 1958 around the lambda calculus. Haskell, considered by many as one of the purest functional programming languages, was developed by Simon Peyton Jones, Paul Houdak, Phil Wadler and others in the late 1980s and early 90s. Many established languages such as C++ and Java and many more recent languages such as Python, Ruby, and JavaScript have adopted lambda expressions as anonymous functions from the lambda calculus.

Because of its simplicity, lambda calculus is a very useful tool for the study and analysis of programming languages.

Concrete Syntax

The concrete syntax of the lambda calculus looks like below:

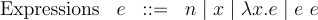
It only has variables x, constants n (akin to values), function abstractions (λx.e), and function applications (e e). This is a tiny subset of the language we have in our Lambda interpreter, but this is all we need to define all computable functions!

A function abstraction is a lambda expression that defines a function. It consists of four parts: a lambda followed by a variable, a period, and then an expression as in λx.e. Here, the variable x is the formal parameter of the function and e is the body of the function. For example, the function abstraction λx.x + 1 defines a function of x that adds x to 1. We say that λx.e binds the variable x in e and that e is the scope of the variable. Parentheses can be added to lambda expressions for clarity. Thus, we could have written this function abstraction as λx.(x + 1).

Note, we are not using the Racket syntax. This example does not illustrate the pure lambda calculus, because it uses the + operator, which is not part of the pure lambda calculus; however, this example is easier to understand than a pure lambda calculus example.

A function application, often called a lambda application, consists of an expression followed by an expression: e e. The first expression is a function abstraction and the second expression is the argument to which the function is applied. All functions in lambda calculus have exactly one argument. For example, the lambda expression λx.x + 1 2 or better written as λx.(x + 1) 2 is an application of the function λx. (x + 1) to the argument 2.

Function application associates left-to-right; thus, f g h = (f g) h and it also binds more tightly than λ; thus, λx. f g x = (λx. (f g)x).

Functions in the lambda calculus are first-class citizens; that is to say, functions can be used as arguments to functions and functions can return functions as results.

Currying / Multi-argument functions

All functions in lambda calculus are prefix and take exactly one argument. So how do we represent functions that take multiple arguments?

If we want to apply a function to more than one argument, we can use a technique called currying that treats a function applied to more than one argument to a sequence of applications of one-argument functions.

For example, to express the sum of two numbers x and y we can write λx.λy.x + y. To use this functions we have to apply it to two arguments in sequence. For example, to add 1 and 2, we use ((λx.λy.x + y) 1) 2. This is equivalent to a function in a programming language that allows multiple arguments. For example, in Racket and (our Lambda language syntax) the curried version looks like (((λ (x) (λ (y) (+ x y))) 1) 2), which is equivalent to ((λ (x y) (+ x y)) 1 2).

Free and Bound Variables

In the function definition λx.x the variable x in the body of the definition (the second x) is bound because its first occurrence in the definition is λx. A variable that is not bound in expression e is said to be free in e. For example, in the function (λx.xy), the variable x in the body of the function is bound and the variable y is free.

Every variable in a lambda expression is either bound or free. Bound and free variables have quite a different status in functions.

• In the expression (λx.x)(λy.yx):
  • The variable x in the body of the leftmost expression is bound to the first lambda.
  • The variable y in the body of the second expression is bound to the second lambda.
  • The variable x in the body of the second expression is free.
  • Note that x in second expression is independent of the x in the first expression.
• In the expression (λx.xy)(λy.y):
  • The variable y in the body of the leftmost expression is free.
  • The variable y in the body of the second expression is bound to the second lambda.

Given an expression e, the following rules define FV(e), the set of free variables in e:

• If e is a variable x, then FV(e) = {x}.
• If e is of the form λx.y, then FV(e) = FV(y) − {x}.
• If e is of the form x y, then FV(e) = FV(x) ∪ FV(y), i.e., the union of two sets.

An expression with no free variables is said to be closed.

Beta Reductions

A function application λx.e y is evaluated by substituting the argument y for all free occurrences of the formal parameter x in the body e of the function definition λx.e. We will use the notation [y/x]e to indicate that y is to be substituted for all free occurrences of x in the expression e. This substitution is the same as the one presented in let bindings. For example:

• (λx.x)y reduces to [y/x]x = y.
• (λx.xzx)y reduces to [y/x]xzx = yzy.
• (λx.z)y reduces to [y/x]z = z since the formal parameter x does not appear in the body z.

This substitution in a function application is called a beta reduction. If we use substitution to transform e1 to e2, we say e1 reduces to e2 in one step. In general, (λx.e) y reduces to [y/x]e means that applying the function (λx.e) to the argument expression y reduces to the expression [y/x]e where the argument expression y is substituted for the function’s formal parameter x in the function body e.

A lambda calculus expression (aka a “program”) is “run” by computing a final result by repeatedly applying beta reductions, until we cannot reduce it any further. It is the reflexive and transitive closure of the term under substitution, i.e., zero or more applications of beta reductions. For example:

• (λx.x)y reduces to y (illustrating that λx.x is the identity function).
• (λx.xx)(λy.y) reduces to (λy.y)(λy.y) reduces to (λy.y); thus, we can say (λx.xx)(λy.y) evaluates to (λy.y). Note that here we have applied a function to a function as an argument and the result is a function.

Below is the behavior of beta reduction defined formally as the β function. The first argument is a term in which variables will be substituted. The second argument y is the variable whose occurence will be substituted. Finally, N is the term that will be substituted in places of y.

Variables are substituted only when there names match.

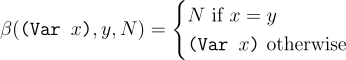
For lambda terms, if the argument x is the same name as the variable y, there is no need to substitute in the body (as the lambda term rebinds the variable). Conversely, there is a possiblity that x might occur in the lambda body e and in the expression N. In that case, we check if there are any free occurences of x in N. If there is none, the result is the substituted body of the lambda. Finally, if there are free occurences, we first alpha rename the free variables with the same name in e and then use the renamed term for substitution.

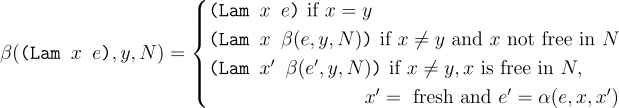
Function application is relatively simple. We just need to beta reduce on both the function and the argument expression.

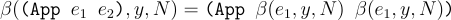
Alpha Reductions

Note that a variable may occur more than once in some lambda expression; some occurrences may be free and some may be bound, so the variable itself is both free and bound in the expression, but each individual occurrence is either free or bound (not both). For example, the free variables of the following lambda expression are {y,x} and the bound variables are {y}:

        (λx.y)(λy.y x)
            |     | |
            |     | free
           free   |
                bound

To tackle this, given lambda expression (λx.e1) e2 instead of replacing all occurrences of x in e1 with e2, we replace all occurrences of x that are free in e1 with e2. For example:

               +----- e1 --------+
               |                 |
           (λx. x + ((λx.x + 1)3)) 2
                |        |
                |        |
               free    bound
               in e1   in e1

             => 2 + ((λx.x + 1)3)

The issue here is that a variable y that is free in the original argument to a lambda expression becomes bound after rewriting (using that argument to replace all instances of the formal parameter), because it is put into the scope of a lambda with a formal that happens also to be named y:

    ((λx.λy.x)y)z
              |
              |
              free, but gets bound after application 

To solve this, we use a technique called alpha reduction. The key idea is that formal parameter names are unimportant; so rename them as needed to avoid capture. Alpha reduction is used to modify expressions of the form λx.e. It renames all the occurrences of x that are free in e to some other variable z that does not occur in e (and then λx is changed to λz). For example, consider λx.λy.x + y (this is of the form λx.e). Variable z is not in e, so we can rename x to z; i.e., λx.λy.x + y alpha-reduces to λz.λy.z + y.

Here is alpha reduction formally defined as the α function.

For a variable, it is renamed only if it has the same name as the variable being renamed.

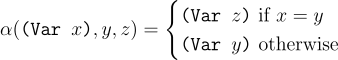
For lambda terms, if the variable being replaced is captured, then there is no need to rename. Otherwise, it is renamed in the body of the lambda term.

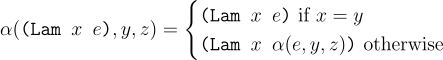
For function application, the rename is carried out both in the function and the argument.

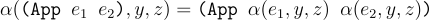
Evaluating a Lambda Expression

A lambda calculus expression can be thought of as a program which can be executed by evaluating it. Evaluation is done by repeatedly finding a reducible expression (called a redex) and reducing it by a function evaluation until there are no more redexes.

Example 1: The lambda expression (λx.x) y in its entirety is a redex that reduces to y.

Example 2: The lambda expression (+ (* 1 2) (− 4 3)) has two redexes: (* 1 2) and (− 4 3). If we choose to reduce the first redex, we get (+ 2 (− 4 3)). We can then reduce (+ 2 (− 4 3)) to get (+ 2 1). Finally we can reduce (+ 2 1) to get 3.

The term beta reduction is perhaps misleading, since doing beta-reduction does not always produce a smaller lambda expression. In fact, a beta-reduction can:

• decrease,
• increase,
• not change

the length of a lambda expression. Below are some examples. In the first example, the result of the beta-reduction is the same as the input (so the size doesn’t change); in the second example, the lambda expression gets longer and longer; and in the third example, the result first gets longer, and then gets shorter.

• (λx.xx)(λx.xx) reduces to (λx.xx)(λx.xx)
• (λx.xxx)(λx.xxx) reduces to (λx.xxx)(λx.xxx)(λx.xxx) reduces to (λx.xxx)(λx.xxx)(λx.xxx)(λx.xxx)
• (λx.xx)(λa.λb.bbb) reduces to (λa.λb.bbb)(λa.λb.bbb) reduces to λb.bbb

Normal Form

An expression containing no possible beta reductions is said to be in normal form. A normal form expression is one containing no redexes (reducible expressions), that is, one with no subexpressions of the form (λx.e) y. Examples of normal form expressions:

• x where x is a variable.
• x e where x is a variable and e is a normal form expression.
• λx.e where x is a variable and e is a normal form expression.

The expression (λx.x x) (λx.x x) does not have a normal form because the entire expression is a redex that always evaluates to itself. We can think of this expression as a representation for an infinite loop.

Relating this to our interpreter

For the language we implemented in class, we did not use alpha and beta reductions because our interpreter used an environment. This is the same distinction we saw in substitution vs. environments for let bindings, but in a more general form! Alpha and beta reduction give us a simple mathematical defintion to define how programs in the lambda calculus should be evaluated simply by substituting. It also allows us explore different styles in which a program can be reduced to a value and how it might change the behavior of programs. The next section discusses this.

Reduction Strategy

A program can be reduced to find the resulting value. In other words, it takes a reducible expression, or redex, and reduces it using the reduction rules. However, here also multiple choices are available when reducing a term and a reduction strategy specifies the order in which beta reductions are made.

Some reduction orders for a lambda expression may yield a normal form while other orders may not. For example, consider the given expression

(λx.1)((λx.x x)(λx.x x))

This expression has two redexes:

1. The entire expression is a redex in which we can apply the function (λx.1) to the argument ((λx.x x)(λx.x x)) to yield the normal form 1. This redex is the leftmost outermost redex in the given expression.
2. The subexpression ((λx.x x)(λx.x x)) is also a redex in which we can apply the function (λx.x x) to the argument (λx.x x). Note that this redex is the leftmost innermost redex in the given expression. But if we evaluate this redex we get same subexpression: (λx.x x)(λx.x x) → (λx.x x)(λx.x x). Thus, continuing to evaluate the leftmost innermost redex will not terminate and no normal form will result.

As a second example, consider the expression

(λx. λy. y)((λz.z z)(λz.z z))

This expression has two redexes:

1. The entire expression is a redex in which we apply the function (λx. λy. y) to the argument ((λz.z z)(λz.z z)) to yield the normal form (λy. y). This redex is the leftmost outermost redex in the given expression.
2. The subexpression ((λz.z z)(λz.z z)) is also a redex in which we can apply the function (λz.z z) to the argument (λz.z z). Note that this redex is the leftmost innermost redex in the given expression. But if we evaluate this redex we get same subexpression: ((λz.z z)(λz.z z)) → ((λz.z z)(λz.z z)). Thus, continuing to evaluate the leftmost innermost redex will not terminate and no normal form will result.

In general, there are two orders for evaluating lambda expressions:

• Applicative order: Broadly, replace the bound variables with the value of the argument expression. The leftmost innermost redex is always reduced first. Intuitively this means a function’s arguments are always reduced before the function itself. Often this is known as call-by-value.
• Normal Order: Replace bound variables by unevaluated argument expressions. The leftmost outermost redex is always reduced first and the arguments are substituted into the body before reduction. Often this is known as call-by-name.

Encoding programs in Lambda Calculus

So far we look at how we can compute with lambda expressions. Turns out we can encode any behavior of a computable program in a lambda expression. This means we can encode all language features we developed until now (or any feature you want from your favorite language) as lambda expressions!

Encoding Let Bindings

Let us recall what a let binding like (let ((x e1)) e2) did: it bound e1 to x, and made x a bound variable in the expression e2. This is infact what lambdas do as well.

A lambda term ((λx.e2) e1) is exactly the same—it evaluates to e2, while binding x to e1. We can actually run this through our interpreter or even Racket to confirm it is correct:

> (interp-err (parse-prog '((let ((x  5))
                              (+ x 1)))))
6

> (interp-err (parse-prog '(((λ (x) (+ x 1)) 5))))
6

Encoding Conditionals and Boolean Values

First, let’s consider how to encode a conditional expression: (if p a b) (i.e., the value of the whole expression is either a or b, depending on the value of p). We will represent this conditional expression using a lambda expression of the form: (cond p a b), where cond, p, a and a are all lambda expressions. In particular, cond is a function of 3 arguments that works by applying p to a and b (i.e., p itself chooses a or b):

cond ::= λp.λa.λb.p a b

To make this definition work correctly, we must define the representations of true and false carefully (since the lambda expression p that cond applies to its arguments a and b will reduce to either true or false). In particular, when true is applied to a and b we want it to return a, and when false is applied to a and b we want it to return b. Therefore, we will let true be a function of two arguments that ignores the second argument and returns the first argument, and we’ll let false be a function of two arguments that ignores the first argument and returns the second argument:

true  ::= λx.λy.x
false ::= λx.λy.y

Now let’s consider an example: cond true m n. Note that this expression should evaluate to m. Let’s see if it does (by substituting our definitions for cond and true, and evaluating the resulting expression). The sequence of beta reductions is shown below; in each case, the redex about to be reduced is indicated by underlining the formal parameter and the argument that will be substituted in for that parameter.

   (λp.λa.λb.p a b)(λx.λy.x) m n
=> (λa.λb.(λx.λy.x)a b) m n
=> (λb.(λx.λy.x) m b) n
=> (λx.λy.x) m n
=> (λy.m)n
=> m

We can run such programs through Racket and confirm our understanding is correct:

> (let ((true  (λ (x) (λ (y) x)))
        (false (λ (x) (λ (y) y)))
        (cond  (λ (c) (λ (t) (λ (e) ((c t) e))))))
    (((cond false) 4) 5))
5

> (let ((true  (λ (x) (λ (y) x)))
        (false (λ (x) (λ (y) y)))
        (cond  (λ (c) (λ (t) (λ (e) ((c t) e))))))
    (((cond racket) 4) 5))
4

We can also run this through our interpreter as well to verify our interpreter implements the lambda calculus:

> (interp-err (parse-prog '((let ((true  (λ (x) (λ (y) x)))
                                  (false (λ (x) (λ (y) y)))
                                  (cond  (λ (c) (λ (t) (λ (e) ((c t) e))))))
                              (((cond false) 4) 5))
5

> (interp-err (parse-prog '((let ((true  (λ (x) (λ (y) x)))
                                  (false (λ (x) (λ (y) y)))
                                  (cond  (λ (c) (λ (t) (λ (e) ((c t) e))))))
                              (((cond true) 4) 5))
4

Y-Combinator

We have one final issue to deal with: recursive functions. For example, consider how we wrote the factorial function before:

(define (fact n)
  (if (zero? n) 1
      (* n (fact (- n 1)))))

This crucially relies on the ability to name our functions. Without the ability to call the function fact, how do we recursively call it?

To do this we use the Y-combinator in lambda calculus which is defined as:

λf.(λy.f(y y))(λy.f(y y))

This computes the fix-point of a function, i.e., the result of applying the function repeatedly until it terminates. Assuming you are applying the the Y-combinator to a function g.

   (Y g)
=> (λf.(λy.f(y y))(λy.f(y y)) g)
=> (λy.g(y y)) (λy.g(y y))
=> g((λy.g(y y)) (λy.g(y y)))
=> g (Y g)
=> ...

To actually try this out in Racket, you can enable the lazy version of Racket which is very similar to the call-by-name or the normal order evaluation strategy. To do this change the first line of Racket to use #lang lazy instead of #lang racket.

#lang lazy

(define Y (λ (f) ((λ (x) (f (x x))) (λ (x) (f (x x))))))

(Y (λ (fact)
     (λ (n)
       (if (zero? n) 1
           (* n (fact (- n 1)))))))

Here we updated the definition of factorial such that it takes an argument fact and we use that. Because we evaluate through the Y-combinator this fact argument turns out to be (Y g) term thus calling recursively.

To compute the factorial of a number now:

> ((Y (λ (fact)
        (λ (n)
          (if (zero? n) 1
              (* n (fact (- n 1))))))) 3)
6