Con: A language of conditions

Table of contents

• Multiple types of values
• Concrete Syntax
• Abstract Syntax
• Meaning of Con Programs
• Interpreter for Con
• Correctness

Multiple types of values

Until now our language produced only one kinds of values: integers. While useful for calculating arithmetic expressions, it is quite limiting. Let’s first address it by introducing boolean values into the language. We will call our new language Con. The two values we will add are #t for true and #f for false. These mirror Racket’s boolean values. Adding boolean values is pointless if our language does not allow us to operate over such values. So we will add some operations if, <=, zero?, and and. We’ll describe these operations in detail.

Concrete Syntax

Con extends Arithmetic by these operations we described above. It contains #lang racket followed by a single expression. Our expressions have integers, booleans, and additional operation like and, if, zero? and so on. The grammar of concrete expression is:

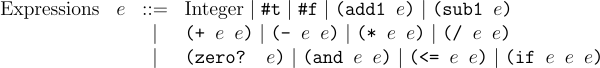
Thus few examples of valid Con programs are:

#lang racket
(+ 42 (sub1 34))

#lang racket
(zero? (- 5 (sub1 6)))

#lang racket
(if (zero? 0) (add1 5) (sub1 5))

Abstract Syntax

The grammar for the abstract syntax of Con is:

We now have a new rule in the grammar for If. Similarly we have extended UnOp and BinOp with zero?, <=, and 'and as appropriate. Crucially, as our language contains both integers and booleans, the Int rule does not exist. Instead, it has been replaced with Val that denotes all values in our language. Thus the above programs will translate to the following abstract syntax:

• (BinOp '+ (Val 42) (UnOp 'sub1 (Val 34)))
• (UnOp 'zero? (BinOp '- (Val 5) (UnOp 'sub1 (Val 6))))
• (If (UnOp 'zero? (Val 0)) (UnOp 'add1 (Val 5)) (UnOp 'sub1 (Val 5)))

We can represent these data types for representing expressions as:

#lang racket

(provide Val UnOp BinOp If)

;; type Expr =
;; | (Val v)
;; | (UnOp u e)
;; | (BinOp b e e)
;; | (If e e e)
;;
;; type UnOp = 'add1 | 'sub1 | 'zero?
;; type BinOp = '+ | '- | '* | '/ | '<= | 'and
(struct Val (v) #:prefab)
(struct UnOp (u e) #:prefab)
(struct BinOp (b e1 e2) #:prefab)
(struct If (e1 e2 e3) #:prefab)

The parser is slightly longer than Arithmetic, but almost similar:

#lang racket

(require "ast.rkt")

(provide parse)

;; S-Expr -> Expr
(define (parse s)
  (match s
    [(? integer?) (Val s)]
    [(? boolean?) (Val s)]
    [(list (? unop? u) e) (UnOp u (parse e))]
    [(list (? binop? b) e1 e2) (BinOp b (parse e1) (parse e2))]
    [`(if ,e1 ,e2 ,e3) (If (parse e1) (parse e2) (parse e3))]
    [_ (error "Parse error!")]))

;; Any -> Boolean
(define (unop? x)
  (memq x '(add1 sub1 zero?)))

;; Any -> Boolean
(define (binop? x)
  (memq x '(+ - * / <= and)))

Meaning of Con Programs

We will define the meaning of Con programs in natural language. We only define the meaning for the new parts of the language here, the old parts of language stays same.

• The meaning of literal values is just the value itself;
• The meaning of zero? is true if the subexpression is 0 or false otherwise;
• The meaning of and is false if the first subexpression is false, otherwise it is the result of the second subexpression;
• The meaning of <= is a test for if the first subexpression is smaller than or equal to the second subexpression;
• Finally, (if e1 e2 e3) means e3 if e1 means false, or e2 otherwise.

We define the operational semantics as before in terms of the relation. Values in our language form the base case in our inductive relation. The rules E-Int, E-True, and E-False show the meaning for integers, #t, and #f respectively.

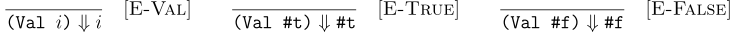
The (zero? e) has two cases. For all expressions e E-ZeroT means #t if e means 0. Alternatively, it means #f (rule E-ZeroF) if e is non-zero.

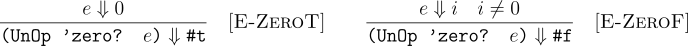
For all expressions e1 and e2, (and e1 e2) #f is in the relation if e1 #f. Otherwise, the relation has the same meaning as e2. Note, how a definition like this works for both booleans and integers. (and #t #t) is #t, (and #f #t) is #f, (and 4 5) is 5, and so on.

For all expressions e1 and e2, (<= e1 e2) #t if e1 means a value less than the meaning of e2.

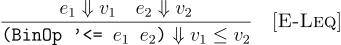
For all expressions e1, e2, and e3, (if e1 e2 e3) e2 is in the relation if e1 means some non-false value. Otherwise (if e1 e2 e3) e3 is in the relation if e1 means false.

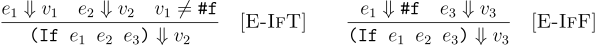
Interpreter for Con

We can now translate these operational semantics rules to the interpreter:

#lang racket

(require rackunit "ast.rkt" "parser.rkt")

(provide interp)

;; interp :: Expr -> Value
(define (interp e)
  (match e
    [(Val v) v]
    [(UnOp u e) (interp-unop u e)]
    [(BinOp b e1 e2) (interp-binop b e1 e2)]
    [(If e1 e2 e3) (interp-if e1 e2 e3)]))

(define (interp-unop u i)
  (match u
    ['add1 (add1 (interp i))]
    ['sub1 (sub1 (interp i))]
    ['zero? (zero? (interp i))]))

(define (interp-binop b i1 i2)
  (match b
    ['+ (+ (interp i1) (interp i2))]
    ['- (- (interp i1) (interp i2))]
    ['* (* (interp i1) (interp i2))]
    ['/ (quotient (interp i1) (interp i2))]
    ['<= (<= (interp i1) (interp i2))]
    ['and (match (interp i1)
            [#f #f]
            [? (interp i2)])]))

(define (interp-if e1 e2 e3)
  (match (interp e1)
    [#f (interp e3)]
    [_  (interp e2)]))

Examples:

> (interp (parse '(+ 42 (sub1 34))))
75
> (interp (parse '(zero? (- 5 (sub1 6)))))
#t
> (interp (parse '(if (zero? 0) (add1 5) (sub1 5))))
6

We can find a one-to-one correspondence between what the interpreter for Con does and the semantics of the language. Whereever shows up in the premise of an operational semantics, it results in recursively calling our interpreter (interp ...). We do not have two cases for handling zero?. We took the easy way out by using the zero? function provided by Racket to build our interpreter. An alternative would be to have a pattern match and return the right value as well. Something similar can be done for and in our language, but I am showing the fully expanded version of the rules than using the built-in and function provided by Racket.

Correctness

We can turn the above examples into automatic test cases:

(module+ test
  (check-eqv? (interp (parse '(+ 42 (sub1 34)))) 75)
  (check-eqv? (interp (parse '(zero? (- 5 (sub1 6))))) #t)
  (check-eqv? (interp (parse '(if (zero? 0) (add1 5) (sub1 5)))) 6))

However, unlike Arithmetic it is easy for us to write malformed programs, i.e., programs that do not mean anything. In other words the meaning of such programs are undefined in our semantics and would most likely crash our interpreter with unexpected error messages or produce unexpected results.

Here are a couple of programs in Con that are valid according to the syntax, but do not mean anything:

> (interp (parse '(add1 #t)))
  add1: contract violation
  expected: number?
  given: #t
> (interp (parse '(<= #t 7)))
  <=: contract violation
  expected: real?
  given: #t

Our interpreter right now does not handle errors gracefully and crashes with errors directly from the underlying Racket runtime.